decisions, rl

view markdown

Some notes on decision theory based on Berkeley’s CS 188 course and “Artificial Intelligence” Russel & Norvig 3rd Edition

game trees - R&N 5.2-5.5

  • like search (adversarial search)
  • minimax algorithm
    • ply - half a move in a tree
    • for multiplayer, the backed-up value of a node n is the vector of the successor state with the highest value for the player choosing at n
    • time complexity - $O(b^m)$
    • space complexity - $O(bm)$ or even $O(m)$
  • alpha-beta pruning cuts in half the exponential depth
    • once we have found out enough about n, we can prune it
    • depends on move-ordering
      • might want to explore best moves = killer moves first
    • transposition table can hash different movesets that are just transpositions of each other
  • imperfect real-time decisions
    • can evaluate nodes with a heuristic and cutoff before reaching goal
    • heuristic uses features
    • want quiescent search - consider if something dramatic will happen in the next ply
      • horizon effect - a position is bad but isn’t apparent for a few moves
      • singular extension - allow searching for certain specific moves that are always good at deeper depths
    • forward pruning - ignore some branches
      • beam search - consider only n best moves
      • PROBCUT prunes some more
  • search vs lookup
    • often just use lookup in the beginning
    • program can solve and just lookup endgames
  • stochastic games
    • include chance nodes
    • change minimax to expectiminimax
    • $O(b^m numRolls^m)$
    • cutoff evaluation function is sensitive to scaling - evaluation function must be a positive linear transformation of the probability of winning from a position
    • can do alpha-beta pruning analog if we assume evaluation function is bounded in some range
    • alternatively, could simulate games with Monte Carlo simulation

utilities / decision theory – R&N 16.1-16.3, mazzonni quant finance book

  • lottery - any function of a random variable
  • utility function - lottery that satisfiers certain properties (e.g. transitivity)
    • expected utility = von Neumann-Morgenstern utility
  • goal: maximize utility by taking actions (focus on single actions)
    • utility function U(s) gives utility of a state
    • actions are probabilistic: $P[RESULT(a)=s’ \vert a,e]$
      • s - state, e - observations, a - action
  • soln: pick action with maximum expected utility
    • expected utility $EU(a\vert e) = \sum_{s’} P(RESULT(a)=s’ \vert a,e) U(s’)$
  • notation
    • A>B - agent prefers A over B
    • A~B - agent is indifferent between A and B
  • preference relation has 6 axioms of utility theory
    1. orderability - A>B, A~B, or A<B
    2. transitivity
    3. continuity
    4. substitutability - can do algebra with preference eqns
    5. monotonicity - if A>B then must prefer higher probability of A than B
    6. decomposability - 2 consecutive lotteries can be compressed into single equivalent lottery
  • these axioms yield a utility function
    • isn’t unique (ex. affine transformation yields new utility function)
    • value function = ordinal utility function - sometimes ranking, numbers not needed
    • agent might not be explicitly maximizing the utility function

utility functions

  • preference elicitation - finds utility function
    • normalized utility to have min and max value
    • assess utility of s by asking agent to choose between s and $(p: \min, (1-p): \max)$
  • people have complicated utility functions
    • ex. micromort - one in a million chance of death
    • ex. QALY - quality-adjusted life year
  • risk
    • agents exhibits monotonic preference for more money
    • gambling has expected monetary value = EMV
    • risk averse = when utility of money is sublinear
      • risk premium = value agent will accept in lieu of lottery = certainty equivalent= insurance premium
    • risk-neutral = linear
    • risk-seeking = supralinear
    • absolute risk aversion $ARA(x) = - \frac{u’‘(x)}{u’(x)} $ : higher is more risk averse
    • relative risk aversion $ARA(x) = - \frac{x \cdot u’‘(x)}{u’(x)} $
  • optimizer’s curse - tendency for E[utility] to be too high because we keep picking high utility randomness
  • normative theory - how idealized agents work
  • descriptive theory - how actual agents work
    • certainty effect - people are drawn to things that are certain
    • ambiguity aversion
    • framing effect - wording can influence people’s judgements
    • anchoring effect - buy middle-tier wine because expensive is there

decision theory / VPI – R&N 16.5 & 16.6

  • note: here we are just making 1 decision
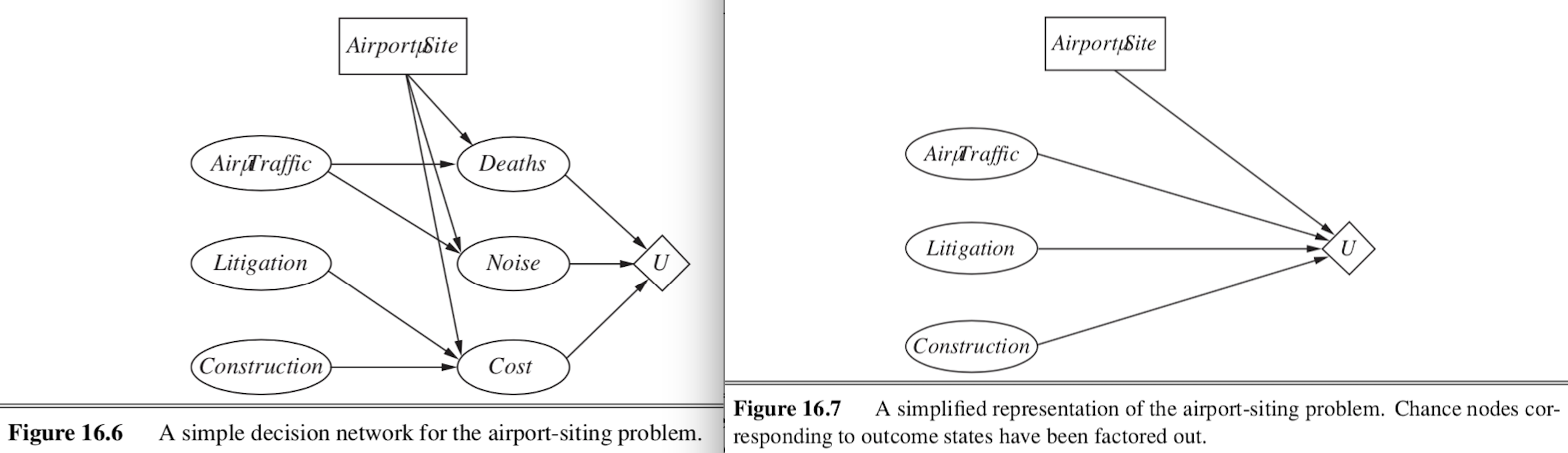
  • decision network (sometimes called influence diagram)
    1. chance nodes - represent RVs (like BN)
    2. decision nodes - points where decision maker has a choice of actions
    3. utility nodes - represent agent’s utility function
  • can ignore chance nodes
    • then action-utility function = Q-function maps directly from actions to utility

decision_nets

  • evaluation
    1. set evidence
    2. for each possible value of decision node
      • set decision node to that value
      • calculate probabilities of parents of utility node
      • calculate resulting utility
    3. return action with highest utility

the value of information

  • information value theory - enables agent to choose what info to acquire
    • observations only affect agent’s belief state
    • value of info = difference in best expected value with/without info
    • maximum $EU(\alpha e) = \underset{a}{\max} \sum_{s’} P(Result(a)=s’ a, e) U(s’)$
  • value of perfect information VPI - assume we can obtain exact evidence for a variable (ex. variable $T=t$)
    • $VPI(T) = \mathbb{E}_{T}\left[ EU(\alpha e, T) \right] - \underbrace{EU(\alpha \vert e)}_{\text{original EU}}$
    • first term expands to $\sum_t P(T=t \vert e) \cdot EU(\alpha \vert e, T=t) $
      • within each of these EU, we take a max over actions
    • VPI not linearly additive, but is order-independent
    • intuition
      • info is more valuable when it is likely to cause a change of plan
      • info is more valuable when the new plan will be much better than the old plan
  • information-gathering agent
    • myopic - greedily obtain evidence which yields highest VPI until some threshold
    • conditional plan - considers more things

mdps and rl - R&N 17.1-17.4

  • sequences of actions
  • fully observable - agent knows its state
  • markov decision process - all these things are given
    • set of states s
    • set of actions a
    • stochastic transition model $P(s’ \vert s,a)$
    • reward function R(s)
      • utility aggregates rewards, for models more complex than mdps reward can be a function of past sequences of actions / observations
  • want policy $\pi (s)$ - what action to do in state s
    • optimal policy yields highest expected utlity
  • optimizing MDP - multiattribute utility theory
    • could sum rewards, but results are infinite
    • instead define objective function (maps infinite sequences of rewards to single real numbers)
      • ex. discounting to prefer earlier rewards (most common)
        • discount reward n steps away by $\gamma^n, 0<\gamma<1$
      • ex. set a finite horizon and sum rewards
        • optimal action in a given state could change over time = nonstationary
      • ex. average reward rate per time step
      • ex. agent is guaranteed to get to terminal state eventually - proper policy
  • expected utility executing $\pi$: $U^\pi (s) = \mathbb E_{s_1,…,s_t}\left[\sum_t \gamma^t R(s_t)\right]$
    • when we use discounted utilities, $\pi$ is independent of starting state
    • $\pi^*(s) = \underset{\pi}{argmax} : U^\pi (s) = \underset{a}{argmax} \sum_{s’} P(s’ \vert s,a) U’(s)$
  • experience replay: instead of learning from samples one by one, want to reduce correlation between subsequent samples
    • take a large batch of samples and sample randomly from it, rather than going sequentially

value iteration

  • value iteration - calculates utility of each state and uses utilities to find optimal policy
    • bellman eqn: $U(s) = R(s) + \gamma : \underset{a}{\max} \sum_{s’} P(s’ \vert s, a) U(s’)$
    • start with arbitrary utilities
    • recalculate several times with Bellman update to approximate solns to bellman eqn
  • value iteration eventually converges
    • contraction - function that brings variables together
      • contraction only has 1 fixed point
      • Bellman update is a contraction on the space of utility vectors and therefore converges
      • error is reduced by factor of $\gamma$ each iteration
    • also, terminating condition - if $ \vert \vert U_{i+1}-U_i \vert \vert < \epsilon (1-\gamma) / \gamma$ then $ \vert \vert U_{i+1}-U \vert \vert <\epsilon$
    • what actually matters is policy loss $ \vert \vert U^{\pi_i}-U \vert \vert $ - the most the agent can lose by executing $\pi_i$ instead of the optimal policy $\pi^*$
      • if $ \vert \vert U_i -U \vert \vert < \epsilon$ then $ \vert \vert U^{\pi_i} - U \vert \vert < 2\epsilon \gamma / (1-\gamma)$

policy iteration

  • another way to find optimal policies
    1. policy evaluation - given a policy $\pi_i$, calculate $U_i=U^{\pi_i}$, the utility of each state if $\pi_i$ were to be executed
      • like value iteration, but with a set policy so there’s no max
      • $U_i(s) = R(s) + \gamma : \sum_{s’} P(s’ \vert s, \pi_i(s)) U_i(s’)$
      • can solve exactly for small spaces, or approximate (set of lin. eqs.)
    2. policy improvement - calculate a new MEU policy $\pi_{i+1}$ using $U_i$
      • same as above, just $\pi^*(s) = \underset{\pi}{argmax} : U^\pi (s) = \underset{a}{argmax} \sum_{s’} P(s’ \vert s,a) U’(s)$
  • asynchronous policy iteration - don’t have to update all states at once

partially observable markov decision processes (POMDP)

  • agent is not sure what state it’s in

  • same elements but add sensor model $P(e \vert s)$

  • have distr $b(s)$ for belief states
    • updates like the HMM: $b’(s’) = \alpha P(e \vert s’) \sum_s P(s’ \vert s, a) b(s)$
    • changes based on observations

  • optimal action depends only on the agent’s current belief state

    • use belief states as the states of an MDP and solve as before
    • changes because state space is now continuous
  • value iteration
    1. expected utility of executing p in belief state is just $b \cdot \alpha_p$ (dot product)
    2. $U(b) = U^{\pi^*}(b)=\underset{p}{\max} : b \cdot \alpha_p$
      • belief space is continuous [0, 1] so we represent it as piecewise linear, and store these discrete lines in memory
        • do this by iterating and keeping any values that are optimal at some point
      • remove dominated plans - generally this is far too inefficient
  • dynamic decision network - online agent

reinforcement learning – R&N 21.1-21.6

  • reinforcement learning - use observed rewards to learn optimal policy for the environment
    • in ch 17, agent had model of environment (P(s’ s, a) and R(s))
  • 2 problems
    • passive - given $\pi$, learn $U^\pi (s)$
    • active - explore states to find utilities and exploit to get highest reward
  • 2 model types, 3 agent designs
    • model-based: can predict next state/reward before taking action (for MDP, requires learning $P(s’ s,a)$)
      • utility-based agent - learns utility function on states
        • requires model of the environment
    • model-free
      • Q-learning agent: learns action-utility function = Q-function maps actions $\to$ utility
      • reflex agent: learns policy that maps directly from states to actions

passive reinforcement learning

  • given policy $\pi$, learn $U^\pi (s) = \mathbb E\left[ \sum_{t=0}^{\infty} \gamma^t R(S_t)\right]$

    • like policy evaluation, but transition model / reward function are unknown
  • direct utility estimation: treat states independently
    • run trials to sample utility
    • average to get expected total reward for each state = expected total reward from each state
  • adaptive dynamic programming (ADP) - sample to estimate transition model $P(s’ s, a)$ and rewards $R(s)$, then plug into Bellman eqn to find $U^\pi(s)$ (plug in at each step)
    • we might want to enforce a prior on the model (two ways)
      1. Bayesian reinforcement learning - assume a prior $P(h)$ on transition model h
        • use prior to calculate $P(h \vert e)$
        • use $P(h e)$ to calculate optimal policy: $\pi^* = \underset{\pi}{argmax} \sum_h P(h \vert e) u_h^\pi$
        • $u_h^\pi$= expected utility over all possible start states, obtained by executing policy $\pi$ in model h
      2. give best outcome in the worst case over H (from robust control theory)
        • $\pi^* = \underset{\pi}{argmax}: \underset{h}{\min} : u_h^\pi$
  • temporal-difference learning - adjust utility estimates towards local equilibrium for correct utilities
    • like an approximation of ADP
    • when we transition $s \to s’$, update $U^\pi(s) = U^\pi (s) + \alpha \left[R(s) - U^\pi (s) + \gamma :U^\pi (s’) \right]$
      • $\alpha$ should decrease over time to converge
    • prioritized sweeping - prefers to make adjustments to states whose likely successors have just undergone a large adjustment in their own utility estimates
      • speeds things up

active reinforcement learning

  • no longer following set policy

    • explore states to find their utilities and exploit model to get highest reward

    • must explore all actions, not just those in the policy

  • bandit problems - determining exploration policy

    • n-armed bandit - pulling n levelers on a slot machine, each with different distr.
    • Gittins index - function of number of pulls / payoff

  • coorect schemes should be GLIE - greedy in the limit of infinite exploration - visits all states infinitely, but eventually become greedy

agent examples

  • ex. choose random action $1/t$ of the time
  • ex. active adp agent
    • give optimistic utility to relatively unexplored states
    • uses exploration function f(u, numTimesVisited) around the sum in the bellman eqn
      • high utilities will propagate
  • ex. active TD agent
    • now must learn transitions (same as adp)
    • update rule same as passive TD

learning action-utility function

  • $U(s) = \underset{a}{\max} : Q(s,a)$
    • ADP version: $Q(s, a) = R(s) + \gamma \sum_{s’} P(s’ s, a) \underset{a’}{\max} Q(s’, a’)$
    • TD version: $Q(s,a) = Q(s,a) + \alpha [R(s) - Q(s,a) + \gamma : \underset{a’}{\max} Q(s’, a’)]$ - this is what is usually referred to as Q-learning
  • SARSA (state-action-reward-state-action) is related: $Q(s,a) = Q(s,a) + \alpha [R(s) + \gamma : Q(s’, a’) - Q(s,a) ]$
    • here, a’ is action actually taken
  • Q-learning is off-policy (only uses best Q-value)
    • more flexible

  • SARSA is on-policy (pays attention to actual policy being followed)

  • can approximate Q-function with something other than a lookup table
    • ex. linear function of parameters $\hat{U}_\theta(s) = \theta_1f_1(s) + … + \theta_n f_n(s)$
      • can learn params online with delta rule = wildrow-hoff rule: $\theta_i = \theta - \alpha : \frac{\partial Loss}{\partial \theta_i}$
  • keep twiddling the policy as long as it improves, then stop
    • store one Q-function (parameterized by $\theta$) for each action
    • ex. $\pi(s) = \underset{a}{\max} : \hat{Q}_\theta (s,a)$
      • this is discontinunous, instead often use stochastic policy representation (ex. softmax for $\pi_\theta (s,a)$)
    • learn $\theta$ that results in good performance
      • Q-learning learns actual Q* function - could be different (scaling factor etc.)
  • to find $\pi$ maximize policy value $p(\theta) = $ expected reward executing $\pi_\theta$
    • could do this with sgd using policy gradient
    • when environment/policy is stochastic, more difficult
      1. could sample mutiple times to compute gradient
      2. REINFORCE algorithm - could approximate gradient at $\theta$ by just sampling at $\theta$: $\nabla_\theta p(\theta) \approx \frac{1}{N} \sum_{j=1}^N \frac{(\nabla_\theta \pi_\theta (s, a_j)) R_j (s)}{\pi_\theta (s, a_j)}$
      3. PEGASUS - correlated sampling - ex. 2 blackjack programs would both be dealt same hands - want to see different policies on same things

planning