computer vision

view markdown

useful packages

  • https://www.cellpose.org/ - cell segmentation
  • Active shape model - Wikipedia
    • intro (cootes 2000)
    • Model-based methods make use of a prior model of what is expected in the image, and typically attempt to find the best match of the model to the data in a new image
    • model
      • requires user-specified landmarks $x$ (e.g. points for eyes/nose on a face)
      • simplest model - use a typical example as a prototype + compare others using correlation
      • invariances: given a set of image coordinates, for all rotations / scales / translations - try them all so that the sum of distances of each shape to the mean is minimized (called Procrustes analysis)
      • shape model learns low-dim model of $x$, maybe using $k$ top bases of PCA
    • inference
      • nearest neighbor: iteratively find transformation + shape model parameters to represent landmarks
      • classification: non-trivial to define a goodness of fit measure for the landmarks - something like distance between points and strongest nearby edges
      • active shape model - for each landmark, look for nearby groundtruth, adapt PCA values, apply reasonable constraints, then iterate
        • improve speed by doing this at large scales before going to more detailed scales
  • snakes - active contour models (kass et al. 1988)
    • deformable spline - pulled towards object contours while internal forces resist deformation

what’s in an image?

  • vision doesn’t exist in isolation - movement
  • three R’s: recognition, reconstruction, reorganization

fundamentals of image formation

projections

  • image I(x,y) projects scene(X, Y, Z)
    • lower case for image, upper case for scene
      • f is a fixed dist. not a function
      • box with pinhole=center of projection, which lets light go through
      • Z axis points out of box, X and Y aligned w/ image plane (x, y)
  • perspective projection - maps 3d points to 2d points through holes
    • perspective projection works for spherical imaging surface - what’s important is 1-1 mapping between rays and pixels
    • natural measure of image size is visual angle
  • orthographic projection - appproximation to perspective when object is relatively far
    • define constant $s = f/Z_0$
    • transform $x = sX, y = sY$

phenomena from perspective projection

  • parallel lines converge to vanishing point (each family has its own vanishing point)
    • pf: point on a ray $[x, y, z] = [A_x, A_y, A_z] + \lambda [D_x, D_y, D_z]$
    • $x = \frac{fX}{Z} = \frac{f \cdot (A_x+\lambda D_X)}{A_z + \lambda D_z}$
    • $\lambda \to \infty \implies \frac{f \cdot \lambda D_x}{\lambda D_z} = \frac{f \cdot D_x}{D_z}$
    • $\implies$ vanishing point coordinates are $fD_x / D_z , f D_y / D_z$
    • not true when $D_z = 0$
    • all vanishing points lie on horizon
  • nearer objects are lower in the image
    • let ground plane be $Y = -h$ (where h is your height)
    • point on ground plane $y = -fh / Z$
  • nearer objects look bigger
  • foreshortening - objects slanted w.r.t line of sight become smaller w/ scaling factor cos $\sigma$ ~ $\sigma$ is angle between line of sight and the surface normal

radiometry

  • irradiance - how much light (photons) are captured in some time interval
    • radiant power / unit area ($W/m^2$)
    • radiance - power in given direction / unit area / unit solid angle
      • L = directional quantity (measured perpendicular to direction of travel)
      • $L = Power / (dA cos \theta \cdot d\Omega)$ where $d\Omega$ is a solid angle (in steradians)
  • irradiance $\propto$ radiance in direction of the camera
  • outgoing radiance of a patch has 3 factors
    • incoming radiance from light source
    • angle between light / camera
    • reflectance properties of patch
  • 2 special cases
    • specular surfaces - outgoing radiance direction obeys angle of incidence
    • lambertian surfaces - outgoing radiance same in all directions
      • albedo * radiance of light * cos(angle)
    • model reflectance as a combination of Lambertian term and specular term
  • also illuminated by reflections of other objects (ray tracing / radiosity)
  • shape-from-shading (SFS) goes from irradiance $\to$ geometry, reflectances, illumination

frequencies and colors

  • contrast sensitivity depends on frequency + color
  • band-pass filtering - use gaussian pyramid
    • pyramid blending
  • eye
    • iris - colored annulus w/ radial muscles
    • pupil - hole (aperture) whose size controlled by iris
    • retina:
  • colors are what is reflected
  • cones (short = blue, medium = green, long = red)
  • metamer - 2 different but indistinguishable spectra
  • color spaces
    • rgb - easy for devices
      • chips tend to be more green
    • hsv (hue, saturation, value)
    • lab (perceptually uniform color space)
  • color constancy - ability to perceive invariant color despite ecological variations
  • camera white balancing (when entire photo is too yellow or something)
    • manual - choose color-neutral object and normalize
    • automatic (AWB)
      • grey world - force average color to grey
      • white world - force brightest object to white

image processing

transformations

  • 2 object properties
    • pose - position and orientation of object w.r.t. the camera (6 numbers - 3 translation, 3 rotation)
    • shape - relative distances of points on the object
      • nonrigid objects can change shape
Transform (most general on top) Constraints Invariants 2d params 3d params
Projective = homography (contains perspective proj.) Ax + t, A nonsingular, homogenous coords parallel -> intersecting 8 (-1 for scale) 15 (-1 for scale)
Affine Ax + t, A nonsingular parallelism, midpoints, intersection 6=4+2 12=9+3
Euclidean = Isometry Ax + t, A orthogonal length, angles, area 3=1+2 6=3+3
Orthogonal (rotation when det = 1 / reflection when det = -1) Ax, A orthogonal   1 3

  • projective transformation = homography

    • homogenous coordinates - use n + 1 coordinates for n-dim space to help us represent points at $\infty$
      • $[x, y] \to [x_1, x_2, x_3]$ with $x = x_1/x_3, y=x_2/x_3$
        • $[x_1, x_2] = \lambda [x_1, x_2] \quad \forall \lambda \neq 0$ - each points is like a line through origin in n + 1 dimensional space
        • even though we added a coordinate, didn’t add a dimension
      • standardize - make third coordinate 1 (then top 2 coordinates are euclidean coordinates)
        • when third coordinate is 0, other points are infinity
        • all 0 disallowed
      • Euclidean line $a_1x + a_2y + a_3=0$ $\iff$ homogenous line $a_1 x_1 + a_2x_2 + a_3 x_3 = 0$
    • perspective maps parallel lines to lines that intersect
    • incidence of points on lines
      • when does a point $[x_1, x_2, x_3]$ lie on a line $[a_1, a_2, a_3]$ (homogenous coordinates)
      • when $\mathbf{x} \cdot \mathbf{a} = 0$
    • cross product gives intersection of any 2 lines
    • representing affine transformations: $\begin{bmatrix}X’\Y’\W’\end{bmatrix} = \begin{bmatrix}a_{11} & a_{12} & t_x\ a_{21} & a_{22} & t_y \ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}X\Y\1\end{bmatrix}$
    • representing perspective projection: $\begin{bmatrix}1 & 0& 0 & 0\ 0 & 1 & 0 & 0 \ 0 & 0 & 1/f & 0 \end{bmatrix} \begin{bmatrix}X\Y\Z \ 1\end{bmatrix} = \begin{bmatrix}X\Y\Z/f\end{bmatrix} = \begin{bmatrix}fX/Z\fY/Z\1\end{bmatrix}$
  • affine transformations
    • affine transformations are a a group
    • examples
      • anisotropic scaling - ex. $\begin{bmatrix}2 & 0 \ 0 & 1 \end{bmatrix}$
      • shear
  • euclidean transformations = isometries = rigid body transform
    • preserves distances between pairs of points: $   \psi(a) - \psi(b)   =   a-b   $
      • ex. translation $\psi(a) = a+t$
    • composition of 2 isometries is an isometry - they are a group
  • orthogonal transformations - preserves inner products $\forall a,b : a \cdot b =a^T A^TA b$
    • $\implies A^TA = I \implies A^T = A^{-1}$
    • $\implies det(A) = \pm 1$
      • 2D
        • really only 1 parameter $ \theta$ (also for the +t)
        • $A = \begin{bmatrix}cos \theta & - sin \theta \ sin \theta & cos \theta \end{bmatrix}$ - rotation, det = +1
        • $A = \begin{bmatrix}cos \theta & sin \theta \ sin \theta & - cos \theta \end{bmatrix}$ - reflection, det = -1
      • 3D
        • really only 3 parameters
        • ex. $A = \begin{bmatrix}cos \theta & - sin \theta & 0 \ sin \theta & cos \theta & 0 \ 0 & 0 & 1\end{bmatrix}$ - rotation, det rotate about z-axis (like before)
  • rotation - orthogonal transformations with det = +1
    • 2D: $\begin{bmatrix}cos \theta & - sin \theta \ sin \theta & cos \theta \end{bmatrix}$
    • 3D: $ \begin{bmatrix}cos \theta & - sin \theta & 0 \ sin \theta & cos \theta & 0 \ 0 & 0 & 1\end{bmatrix}$ (rotate around z-axis)
  • lots of ways to specify angles
    • axis plus amount of rotation - we will use this
    • euler angles
    • quaternions (generalize complex numbers)
  • Roderigues formula - converts: $R = e^{\phi \hat{s}} = I + sin [\phi] : \hat{s} + (1 - cos \phi) \hat{s}^2$
    • $s$ is a unit vector along $w$ and $\phi=   w   t$ is total amount of rotation
    • rotation matrix
      • can replace cross product with matrix multiplication with a skew symmetric $(B^T = -B)$ matrix:
      • $\begin{bmatrix} t_1 \ t_2 \ t_3\end{bmatrix}$ ^ $\begin{bmatrix} x_1 \ x_2 \ x_3 \end{bmatrix} = \begin{bmatrix} t_2 x_3 - t_3 x_2 \ t_3 x_1 - t_1 x_3 \ t_1 x_2 - t_2 x_1\end{bmatrix}$
        • $\hat{t} = [t_\times] = \begin{bmatrix} 0 & -t_3 & t_2 \ t_3 & 0 & -t_1 \ -t_2 & t_1 & 0\end{bmatrix}$
    • proof
      • $\dot{q(t)} = \hat{w} q(t)$
      • $\implies q(t) = e^{\hat{w}t}q(0)$
      • where $e^{\hat{w}t} = I + \hat{w} t + (\hat{w}t)^2 / w! + …$
        • can rewrite in terms above

image preprocessing

  • image is a function from $R^2 \to R$
    • f(x,y) = reflectance(x,y) * illumination(x,y)
  • image histograms - treat each pixel independently
    • better to look at CDF
    • use CDF as mapping to normalize a histogram
    • histogram matching - try to get histograms of all pixels to be same
  • need to map high dynamic range (HDR) to 0-255 by ignoring lots of values
    • do this with long exposure
    • point processing does this transformation independent of position x, y
  • can enhance photos with different functions
    • negative - inverts
    • log - can bring out details if range was too large
    • contrast stretching - stretch the value within a certain range (high contrast has wide histogram of values)
  • sampling
    • sample and write function’s value at many points
    • reconstruction - make samples back into continuous function
    • ex. audio -> digital -> audio
    • undersampling loses information
    • aliasing - signals traveling in disguise as other frequencies
    • antialiasing
      • can sample more often
      • make signal less wiggly by removing high frequencies first
  • filtering
    • lowpass filter - removes high frequencies
    • linear filtering - can be modeled by convolution
    • cross correlation - what cnns do, dot product between kernel and neighborhood
      • sobel filter is edge detector
    • gaussian filter - blur, better than just box blur
      • rule of thumb - set filter width to about 6 $\sigma$
      • removes high-frequency components
    • convolution - cross-correlation where filter is flipped horizontally and vertically
      • commutative and associative
      • convolution theorem: $F[g*h] = F[g]F[h]$ where F is Fourier, * is convolution
        • convolution in spatial domain = multiplication in frequency domain
  • resizing
    • Gaussian (lowpass) then subsample to avoid aliasing
    • image pyramid - called pyramid because you can subsample after you blur each time
      • whole pyramid isn’t much bigger than original image
      • collapse pyramid - keep upsampling and adding
      • good for template matching, search over translations
  • sharpening - add back the high frequencies you remove by blurring (laplacian pyramid):

edges + templates

  • edge - place of rapid change in the image intensity function

  • solns

    • smooth first, then take gradient
    • gradient first then smooth gives same results (linear operations are interchangeable)

  • derivative theorem of convolution - differentiation can also be though of as convolution

    • can convolve with deriv of gaussian
    • can give orientation of edges
  • tradeoff between smoothing (denoising) and good edge localization (not getting blurry edges)
  • image gradient looks like edges

  • canny edge detector

    1. filter image w/ deriv of Gaussian
    2. find magnitude + orientation of gradient
    3. non-maximum suppression - does thinning, check if pixel is local maxima
      • anything that’s not a local maximum is set to 0
      • on line direction, require a weighted average to interpolate between points (bilinear interpolation = average on edges, then average those points)
    4. hysteresis thresholding - high threshold to start edge curves then low threshold to continue them
  • Scale-space and edge detection using anisotropic diffusion (perona & malik 1990)
    • introduces anisotropic diffusion (see wiki page) - removes image noise without removing content
    • produces series of images, similar to repeatedly convolving with Gaussian
  • filter review
    • smoothing
      • no negative values
      • should sum to 1 (constant response on constant)
    • derivative
      • must have negative values
      • should sum to 0 (0 response on constant)
        • intuitive to have positive sum to +1, negative sum to -1
  • matching with filters (increasing accuracy, but slower)
    • ex. zero-mean filter subtract mean of patch from patch (otherwise might just match brightest regions)
    • ex. SSD - L2 norm with filter
      • doesn’t deal well with intensities
    • ex. normalized cross-correlation
  • recognition
    • instance - “find me this particular chair”
      • simple template matching can work
    • category - “find me all chairs”

texture

  • texture - non-countable stuff
    • related to material, but different
  • texture analysis - compare 2 things, see if they’re made of same stuff
    • pioneered by bela julesz
    • random dot stereograms - eyes can find subtle differences in randomness if fed to different eyes
    • human vision sensitive to some difference types, but not others
  • easy to classify textures based on v1 gabor-like features
  • can make histogram of filter response histograms - convolve filter with image and then treat each pixel independently
  • heeger & bergen siggraph 95 - given texture, want to make more of that texture
    • start with noise
    • match histograms of noise with each of your filter responses
    • combine them back together to make an image
    • repeat this iteratively
  • simoncelli + portilla 98 - also match 2nd order statistics (match filters pairwise)
    • much harder, but works better
  • texton histogram matching - classify images
    • use “computational version of textons” - histograms of joint responses
      • like bag of words but with “visual words”
      • won’t get patches with exact same distribution, so need to extract good “words”
      • define words as k-means of features from 10x10 patches
        • features could be raw pixels
        • gabor representation ~10 dimensional vector
        • SIFT features: histogram set of oriented filters within each box of grid
        • HOG features
        • usually cluster over a bunch of images
        • invariance - ex. blur signal
    • each image patch -> a k-means cluster so image -> histogram
    • then just do nearest neighbor on this histogram (chi-squared test is good metric)
  • object recognition is really texture recognition
  • all methods follow these steps
    • compute low-level features
    • aggregate features - k-means, pool histogram
    • use as visual representation
  • why these filters - sparse coding (data driven find filters)

optical flow

  • simplifying assumption - world doesn’t move, camera moves
    • lets us always use projection relationship $x, y = -Xf/Z, -Yf/Z$
  • optical flow - movement in the image plane
    • square of points moves out as you get closer
      • as you move towards something, the center doesn’t change
      • things closer to you change faster
    • if you move left / right points move in opposite direction
      • rotations also appear to move opposite to way you turn your head
  • equations: relate optical flow in image to world coords
    • optical flow at $(u, v) = (\Delta x / \Delta t, \Delta y/ \Delta t)$ in time $\Delta t$
      • function in image space (produces vector field)
    • $\begin{bmatrix} \dot{X}\ \dot{Y} \ \dot{Z} \end{bmatrix} = -t -\omega \times \begin{bmatrix} X \ Y \ Z\end{bmatrix} \implies \begin{bmatrix} \dot{x}\ \dot{y}\end{bmatrix}= \frac{1}{Z} \begin{bmatrix} -1 & 0 & x\ 0 & 1 & y\end{bmatrix} \begin{bmatrix} t_x \ t_y \ t_z \end{bmatrix}+ \begin{bmatrix} xy & -(1+x^2) & y \ 1+y^2 & -xy & -x\end{bmatrix}\begin{bmatrix} \omega_x \ \omega_y \ \omega_z\end{bmatrix}$
    • decomposed into translation component + rotation component
    • $t_z / Z$ is time to impact for a point
  • translational component of flow fields is more important - tells us $Z(x, y)$ and translation $t$
  • we can compute the time to contact
  • this is a key to what is used in video compression

cogsci / neuro

psychophysics

  • julesz search experiment
    • “pop-out” effect of certain shapes (e.g. triangles but not others)
    • axiom 1: human vision has 2 modes
      • preattentive vision - parallel, instantaneous (~100-200 ms)
        • large visual field, no scrutiny
        • surprisingly large amount of what we do
        • ex. sensitive to size/width, orientation changes
      • attentive vision - serial search with small focal attention in 50 ms steps
    • axiom 2: textons are the fundamental elements in preattentive vision
      • texton is invariant in preattentive vision
      • ex. elongated blobs (rectangles, ellipses, line segments w/ orientation/width/length)
      • ex. terminators - ends of line segments
      • crossing of line segments
  • julesz conjecture (not quite true) - textures can’t be spontaneously discriminated if they have same first-order + second-order statistics (ex. density)
  • humans can saccade to correct place in object detection really fast (150 ms - Kirchner & Thorpe, 2006)
    • still in preattentive regime
    • can also do object detection after seeing image for only 40 ms

neurophysiology

  • on-center off-surround - looks like Laplacian of a Gaussian
    • horizontal cell “like convolution”
  • LGN does quick processing
  • hubel & wiesel - single-cell recording from visual cortex in v1
  • 3 v1 cell classes
    • simple cells - sensitive to oriented lines
      • oriented Gaussian derivatives
      • some were end-stopped
    • complex cells - simple cells with some shift invariance (oriented lines but with shifts)
      • could do this with maxpool on simple cells
    • hypercomplex cells (less common) - complex cell, but only lines of certain length
  • retinotopy - radiation stain on retina maintained radiation image
  • hypercolumn - cells of different orientations, scales grouped close together for a location

perceptual organization

  • max werthermian - we perceive things not numbers
  • principles: grouping, element connectedness
  • figure-ground organization: surroundedness, size, orientation, contrast, symmetry, convexity
  • gestalt - we see based on context

correspondence + applications (steropsis, optical flow, sfm)

binocular steropsis

  • stereopsis - perception of depth
  • disparity - difference in image between eyes
    • this signals depth (0 disparity at infinity)
    • measured in pixels (in retina plane) or angle in degrees
    • sign doesn’t really matter
  • active stereopsis - one projector and one camera vs passive (ex. eyes)
    • active uses more energy
    • ex. kinect - measure / triangulate
      • worse outside
    • ex. lidar - time of light - see how long it takes for light to bounce back
  • 3 types of 2-camera configurations: single point, parallel axes, general case

single point of fixation (common in eyes)

  • fixation point has 0 disparity
    • humans do this to put things in the fovea
  • use coordinates of cyclopean eye
  • vergence movement - look at close / far point on same line
    • change angle of convergence (goes to 0 at $\infty$)
      • disparity = $ 2 \delta \theta = b \cdot \delta Z / Z^2$ where b - distance between eyes, $\delta Z$ - change in depth, Z - depth
      • epth_disparit
        • b - distance between eyes, $\delta$ - change in depth, Z - depth
  • version movement - change direction of gaze
    • forms Vieth-Muller circle - points lie on same circle with eyes
      • cyclopean eye isn’t on circle, but close enough
      • disparity of P’ = $\alpha - \beta = 0$ on Vieth-Muller circle
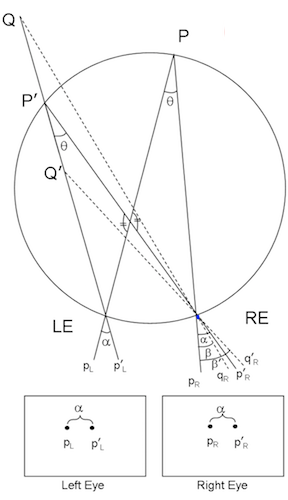
      • ieth_mulle

optical axes parallel (common in robots)

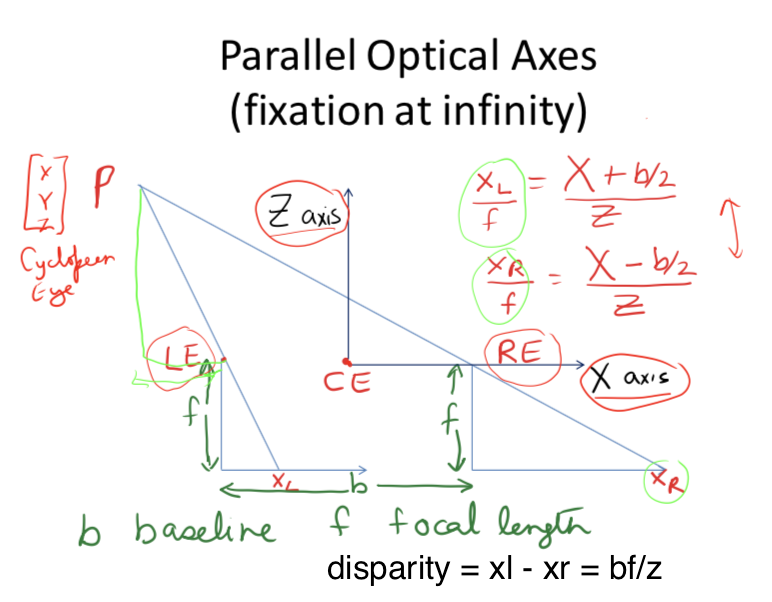
  • isparity_paralle
  • disparity $d = x_l - x_r = bf/Z$
  • error $ \delta Z = \frac{Z^2 \delta d }{bf}$
  • parallax - effect where near objects move when you move but far don’t

general case (ex. reconstruct from lots of photos)

  • given n point correspondences, estimate rotation matrix R, translation t, and depths at the n points

    • more difficult - don’t know coordinates / rotations of different cameras

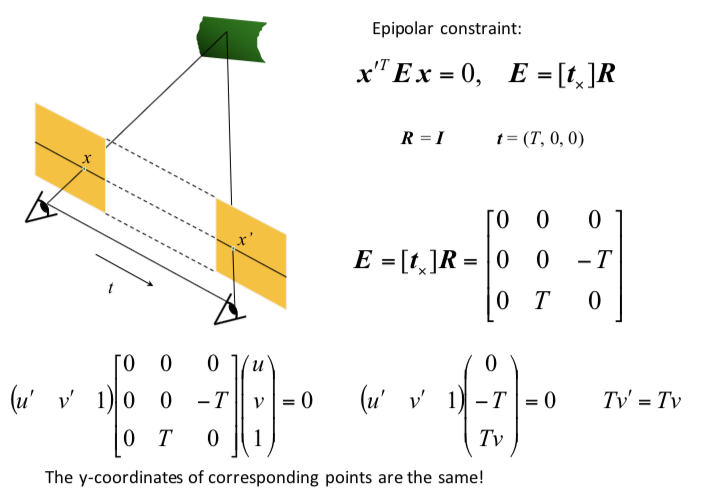
  • epipolar plane - contains cameras, point of fixation

    • different epipolar planes, but all contain line between cameras
    • $\vec{c_1 c_2}$ is on all epipolar planes
    • each image plane has corresponding epipolar line - intersection of epipolar plane with image plane
      • epipole - intersection of $\vec{c_1 c_2}$ and image plane
        • pipolar

  • structure from motion problem: given n corresponding projections $(x_i, y_i)$ in both cameras, find $(X_i, Y_i, Z_i)$ by estimating R, t: Longuet-Higgins 8-point algorithm - overall minimizing re-projection error (basically minimizes least squares = bundle adjustment)

    • find $n (\geq 8)$ corresponding points
    • estimate essential matrix $E = \hat{T} R$ (converts between points in normalized image coords - origin at optical center)
      • fundamental matrix F corresponds between points in pixel coordinates (more degrees of freedom, coordinates not calibrated )
      • essential matrix constraint: $x_1, x_2$ homogoneous coordinates of $M_1, M_2 \implies x_2^T \hat{T} R x_1 = 0$
        • 6 or 5 dof; 3 dof for rotation, 3 dof for translation. up to a scale, so 1 dof is removed
        • $t = c_2 - c_1, x_2$ in second camera coords, $Rx_1$ moves 1st camera coords to second camera coords
      • need at least 8 pairs of corresponding points to estimate E (since E has 8 entries up to scale)
        • if they’re all coplanar, etc doesn’t always work (need them to be independent)
    • extract (R, t)
    • triangulation

solving for stereo correspondence

  • stereo correspondence = stereo matching: given point in one image, find corresponding point in 2nd image
  • basic stereo matching algorithm
    • stereo image rectification - transform images so that image planes are parallel
      • now, epipolar lines are horizontal scan lines
      • do this by using a few points to estimate R, t
    • for each pixel in 1st image
      • find corresponding epipolar line in 2nd image
      • correspondence search: search this line and pick best match
    • simple ex. parallel optical axes = assume cameras at same height, same focal lengths $\implies$ epipolar lines are horizontal scan lines
      • aralle
  • correspondence search algorithms (simplest to most complex)
    • assume photo consistency - same points in space will give same brightness of pixels
    • take a window and use metric
      • larger window smoother, less detail
      • metrics
        • minimize L2 norm (SSD)
        • maximize dot product (NCC - normalized cross correlation) - this works a little better because calibration issues could be different
    • failures
      • textureless surfaces
      • occlusions - have to extrapolate the disparity
        • half-occlusion - can’t see from one eye
        • full-occlusion - can’t see from either eye
      • repetitions
      • non-lambertian surfacies, specularities - mirror has different brightness from different angles

optical flow II

  • related to stereo disparity except moving one camera over time
  • aperture problem - looking through certain hole can change perception (ex. see movement in wrong directions)
  • measure correspondence over time
    • for point (x, y, t), optical flow is (u,v) = $(\Delta x / \Delta t, \Delta y / \Delta t)$
  • optical flow constraint equation: $I_x u + I_y v + I_t = 0$
    • assume everything is Lambertian - brightness of any given point will stay the same
    • also add brightness constancy assumption - assume brightness of given point remains constant over short period $I(x_1, y_1, t_1) = I(x_1 + \Delta x, y_1 + \Delta x, t_1 + \Delta t)$

    • here, $I_x = \partial I / \partial x$

    • local constancy of optical flow - assume u and v are same for n points in neighborhood of a pixel
    • rewrite for n points(left matrix is A): $\begin{bmatrix} I_x^1 & I_y^1\ I_x^2 & I_y^2\ \vdots & \vdots \ I_x^n & I_y^n\ \end{bmatrix}\begin{bmatrix} u \ v\end{bmatrix} = - \begin{bmatrix} I_t^1\ I_t^2\ \vdots \ I_t^n\\end{bmatrix}$
      • then solve with least squares $\begin{bmatrix} u \ v\end{bmatrix}=-(A^TA^{-1} A^Tb)$
      • second moment matrix $A^TA$ - need this to be high enough rank

general correspondence + interest points

  • more general correspondence - matching points, patches, edges, or regions across images (not in the same basic image)
    • most important problem - used in steropsis, optical flow, structure from motion
  • 2 ways of finding correspondences
    • align and search - not really used
    • keypoint matching - find keypoint that matches and use everything else
  • 3 steps to kepoint matching: detection, description, matching

detection - identify key points

  • find ‘corners’ with Harris corner detector
  • shift small window and look for large intensity change in multiple directions
    • edge - only changes in one direction
    • compare auto-correlation of window (L2 norm of pixelwise differences)
  • very slow naively - instead look at gradient (Taylor series expansion - second moment matrix M)
    • if gradient isn’t flat, then it’s a corner
  • look at eigenvalues of M
    • eigenvalues tell you about magnitude of change in different directions
    • if same, then circular otherwise elliptical
    • corner - 2 large eigenvalues, similar values
      • edge - 1 eigenvalue larger than other
    • simple way to compute this: $det(M) - \alpha : trace(M)^2$
  • apply max filter to get rid of noise
    • adaptive - want to distribute points across image
  • invariance properties
    • ignores affine intensity change (only uses derivs)
    • ignores translation/rotation
    • does not ignore scale (can fix this by considering multiple scales and taking max)

description - extract vector feature for each key point

  • lots of ways - ex. SIFT, image patches wrt gradient
  • simpler: MOPS
    • take point (x, y), scale (s), and orientation from gradients
    • take downsampled rectangle around this point in proper orientation
  • invariant to things like shape / lighting changes

matching - determine correspondence between 2 views

  • not all key points will match - only match above some threshold
    • ex. criteria: symmetry - only use if a is b’s nearest neighbor and b is a’s nearest neighbor
    • better: David Lowe trick - how much better is 1-NN than 2-NN (e.g. threshold on 1-NN / 2-NN)
  • problem: outliers will destroy fit
  • RANSAC algorithm (random sample consensus) - vote for best transformation
    • repeat this lots of times, pick the match that had the most inliers
      • select n feature pairs at random (n = minimum needed to compute transformation - 4 for homography, 8 for rotation/translation)
      • compute transformation T (exact for homography, or use 8-point algorithm)
      • count inliers (how many things agree with this match)
        • 8-point algorithm / homography check
        • $x^TEx < \epsilon $ for 8-point algorithm or $x^THx < \epsilon$ for homography
    • ate end could recompute least squares H or F on all inliers

correspondence for sfm / instance retrieval

  • sfm (structure for motion) - given many images, simultaneously do 2 things

    • calibration - find camera parameters
    • triangulation - find 3d points from 2d points
  • structure for motion system (ex. photo tourism 2006 paper)
    • camera calibration: determine camera parameters from known 3d points
      • parameters
        1. internal parameters - ex. focal length, optical center, aspect ratio
        2. external parameters - where is the camera
          • only makes sense for multiple cameras
      • approach 1 - solve for projection matrix (which contains all parameters)
        • requires knowing the correspondences between image and 3d points (can use calibration object)
        • least squares to find points from 3x4 projection matrix which projects (X, Y, Z, 1) -> (x, y, 1)
      • approach 2 - solve for parameters
        • translation T, rotation R, focal length f, principle point (xc, yc), pixel size (sx, sy)
          • can’t use homography because there are translations with changing depth
          • sometimes camera will just list focal length
        • decompose projection matrix into a matrix dependent on these things
        • nonlinear optimization
    • triangulation - predict 3d points $(X_i, Y_i, Z_i)$ given pixels in multiple cameras $(x_i, y_i)$ and camera parameters $R, t$
      • minimize reprojection error (bundle adjustment): $\sum_i \sum_j \underbrace{w_{ij}}_{\text{indicator var}}\cdot   \underbrace{P(x_i, R_j, t_j)}{\text{pred. im location}} - \underbrace{\begin{bmatrix} u{i, j}\v_{i, j}\end{bmatrix}}_{\text{observed m location}}   ^2$
        • solve for matrix that projects points into 3d coords
  • incremental sfm: start with 2 cameras
    • initial pair should have lots of matches, big baseline (shouldn’t just be a homography)
    • solve with essential matrix
    • then iteratively add cameras and recompute
    • good idea: ignore lots of data since data is cheap in computer vision
  • search for similar images - want to establish correspondence despite lots of changes
    • see how many keypoint matches we get
    • search with inverted file index
      • ex. visual words - cluster the feature descriptors and use these as keys to a dictionary
      • inverted file indexing
      • should be sparse
    • spatial verification - don’t just use visual words, use structure of where the words are
      • want visual words to give similar transformation - RANSAC with some constraint

deep learning

cnns

  • object recognition - visual similarity via labels
  • classification
    • linear boundary -> nearest neighbors
  • neural nets
    • don’t need feature extraction step
    • high capacity (like nearest neighbors)
    • still very fast test time
    • good at high dimensional noisy inputs (vision + audio)
  • pooling - kind of robust to exact locations
    • a lot like blurring / downsampling
    • everyone now uses maxpooling
  • history: lenet 1998
    • neurocognition (fukushima 1980) - unsupervised
    • convolutional neural nets (lecun et al) - supervised
    • alexnet 2012
      • used norm layers (still common?)
    • resnet 2015
      • 152 layers
      • 3x3s with skip layers
  • like nonparametric - number of params is close to number of data points
  • network representations learn a lot
    • zeiler-fergus - supercategories are learned to be separated, even though only given single class lavels
    • nearest neighbors in embedding spaces learn things like pose
    • can be used for transfer learning
  • fancy architectures - not just a classifier
    • siamese nets
      • ex. want to compare two things (ex. surveillance) - check if 2 people are the same (even w/ sunglasses)
      • ex. connect pictures to amazon pictures
        • embed things and make loss function distance between real pics and amazon pics + make different things farther up to some margin
      • ex. searching across categories
    • multi-modal
      • ex. could look at repr. between image and caption
    • semi-supervised
      • context as supervision - from word predict neighbors
      • predict neighboring patch from 8 patches in image
    • multi-task
      • many tasks / many losses at once - everything will get better at once
    • differentiable programming - any nets that form a DAG
      • if there are cycles (RNN), unroll it
    • fully convolutional
      • works on different sizes
      • this lets us have things per pixel, not per image (ex. semantic segmentation, colorization)
      • usually use skip connections

image segmentation

  • consistency - 2 segmentations consistent when they can be explained by same segmentation tree
    • percept tree - describe what’s in an image using a tree
  • evaluation - how to correspond boundaries?
    • min-cost assignment on bipartite graph=bigraph - connections only between groundtruth, signal: bigraph
  • ex. for each pixel predict if it’s on a boundary by looking at window around it
    • proximity cue
    • boundary cues: brightness gradient, color gradient, texture gradient (gabor responses)
      • look for sharp change in the property
    • region cue - patch similarity
      • proximity
      • graph partitioning
    • learn cue combination by fitting linear combination of cues and outputting whether 2 pixels are in same segmentation
  • graph partitioning approach: generate affinity graph from local cues above (with lots of neighbors)
    • normalized cuts - partition so within-group similarity is large and between-group similarity is small
  • deep semantic segmentation - fully convolutional
    • upsampling
      • unpooling - can fill all, always put at top-left
      • max-unpooling - use positions from pooling layer
      • learnable upsampling = deconvolution = upconvolution = fractionally strided convolution = backward strided convolution - transpose the convolution

classification + localization

  • goal: coords (x, y, w, h) for each object + class
  • simple: sliding window and use classifier each time - computationally expensive!
  • region proposals - find blobby image regions likely to contain objects and run (fast)
  • R-CNN - run each region of interest, warped to some size, through CNN
  • Fast R-CNN - get ROIs from last conv layer, so everything is faster / no warping
    • to maintain size, fix number of bins instead of filter sizes (then these bins are adaptively sized) - spatial pyramid pooling layer
  • Faster R-CNN - use region proposal network within network to do region proposals as well
    • train with 4 losses for all things needed
    • region proposal network uses multi-scale anchors and predicts relative to convolution
  • instance segmentation
    • mask-rcnn - keypoint detection then segmentation

learning detection

  • countour detection - predict contour after every conv (at different scales) then interpolate up to get one final output (ICCV 2015)
    • deep supervision helps to aggregate multiscale info
  • semantic segmentation - sliding window
  • classification + localization
    • need to output a bounding box + classify what’s in the box
    • bounding box: regression problem to output box
      • use locations of features
  • feature map
    • location of a feature in a feature map is where it is in the image (with finer localization info accross channels)
    • response of a feature - what it is

modeling figure-ground

  • figure is closer, ground background - affects perception
  • figure/ground datasets
  • local cues
    • edge features: shapemes - prototypical local shapes
    • junction features: line labelling - contour directions with convex/concave images
    • lots of principles
      • surroundedness, size, orientation, constrast, symmetry, convexity, parallelism, lower region, meaningfulness, occlusion, cast shadows, shading
    • global cues
      • want consistency with CRF
      • spectral graph segmentation
      • embedding approach - satisfy pairwise affinities

single-view 3d construction

  • useful for planning, depth, etc.
  • different levels of output (increasing complexity)
    • image depth map
    • scene layout - predict simple shapes of things
    • volumetric 3d - predict 3d binary voxels for which voxels are occupied
      • could approximate these with CAD models, deformable shape models
  • need to use priors of the world
  • (explicit) single-view modeling - assume a model and fit it
    • many classes are very difficult to model explicitly
    • ex. use dominant edges in a few directions to calculate vanishing points and then align things
  • (implicit) single-view prediction - learn model of world data-driven
    • collect data + labels (ex. sensors)
    • train + predict
    • supervision from annotation can be wrong

unsupervised keypoint learning