comp neuro

view markdown

navigation

  • cognitive maps (tolman 1940s) - idea that rats in mazes learn spatial maps
  • place cells (o’keefe 1971) - in the hippocampus - fire to indicate one’s current location
  • remap to new locations
  • grid cells (moser & moser 2005) - in the entorhinal cotex (provides inputs to the hippocampus) - not particular locations but rather hexagonal coordinate system
  • grid cells fire if the mouse is in any location at the vertex (or center) of one of the hexagons
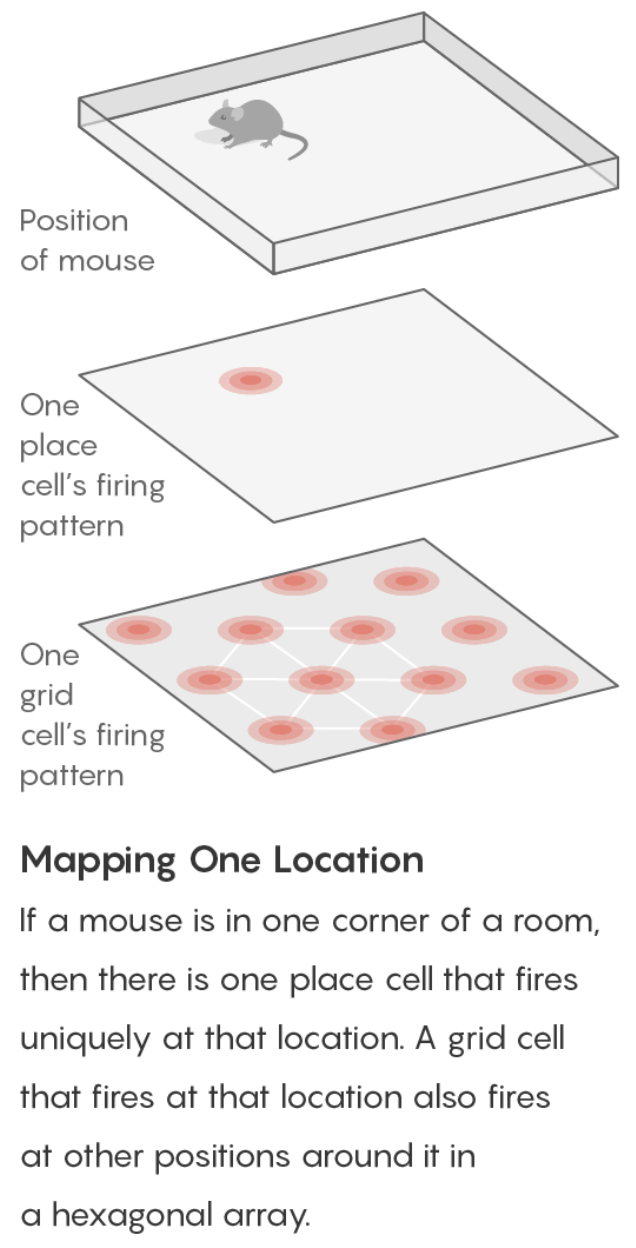
  • Screen Shot 2019-05-10 at 1.25.02 PM
  • there are grid cells with larger/smaller hexagons, different orientations, different offsets
  • can look for grid cells signature in fmri: https://www.nature.com/articles/nature08704
  • other places with grid cell-like behavior
  • eye movement task
  • some evidence for “time cells” like place cells for time
  • sound frequency task https://www.nature.com/articles/nature21692
  • 2d “bird space” task

high-dimensional computing

  • high-level overview
    • current inspiration has all come from single neurons at a time - hd computing is going past this
    • the brain’s circuits are high-dimensional
    • elements are stochastic not deterministic
    • can learn from experience
    • no 2 brains are alike yet they exhibit the same behavior
  • basic question of comp neuro: what kind of computing can explain behavior produced by spike trains?
    • recognizing ppl by how they look, sound, or behave
    • learning from examples
    • remembering things going back to childhood
    • communicating with language
  • HD computing overview paper
    • in these high dimensions, most points are close to equidistant from one another (L1 distance), and are approximately orthogonal (dot product is 0)
    • memory
      • heteroassociative - can return stored X based on its address A
      • autoassociative - can return stored X based on a noisy version of X (since it is a point attractor), maybe with some iteration
        • this adds robustness to the memory
        • this also removes the need for addresses altogether

definitions

  • what is hd computing?
    • compute with random high-dim vectors
    • ex. 10k vectors A, B of +1/-1 (also extends to real / complex vectors)
  • 3 operations
    • addition: A + B = (0, 0, 2, 0, 2,-2, 0, ….)
    • multiplication: A * B = (-1, -1, -1, 1, 1, -1, 1, …) - this is XOR
      • want this to be invertible, dsitribute over addition, preserve distance, and be dissimilar to the vectors being multiplied
      • number of ones after multiplication is the distance between the two original vectors
      • can represent a dissimilar set vector by using multiplication
    • permutation: shuffles values
      • ex. rotate (bit shift with wrapping around)
      • multiply by rotation matrix (where each row and col contain exactly one 1)
      • can think of permutation as a list of numbers 1, 2, …, n in permuted order
      • many properties similar to multiplication
      • random permutation randomizes
  • basic operations
    • weighting by a scalar
    • similarity = dot product (sometimes normalized)
      • A $\cdot$ A = 10k
      • A $\cdot$ A = 0 (orthogonal)
      • in high-dim spaces, almost all pairs of vectors are dissimilar A $\cdot$ B = 0
      • goal: similar meanings should have large similarity
    • normalization
      • for binary vectors, just take the sign
      • for non-binary vectors, scalar weight
  • data structures
  • these operations allow for encoding all normal data structures: sets, sequences, lists, databases
    • set - can represent with a sum (since the sum is similar to all the vectors)
      • can find a stored set using any element
      • if we don’t store the sum, can probe with the sum and keep subtracting the vectors we find
    • multiset = bag (stores set with frequency counts) - can store things with order by adding them multiple times, but hard to actually retrieve frequencies
    • sequence - could have each element be an address pointing to the next element
      • problem - hard to represent sequences that share a subsequence (could have pointers which skip over the subsquence)
      • soln: index elements based on permuted sums
        • can look up an element based on previous element or previous string of elements
      • could do some kind of weighting also
    • pairs - could just multiply (XOR), but then get some weird things, e.g. A * A = 0
      • instead, permute then multiply
      • can use these to index (address, value) pairs and make more complex data structures
    • named tuples - have smth like (name: x, date: m, age: y) and store as holistic vector $H = N*X + D * M + A * Y$
      • individual attribute value can be retrieved using vector for individual key
    • representation substituting is a little trickier….
      • we blur what is a value and whit is a variable
      • can do this for a pair or for a named tuple with new values
        • this doesn’t always work
  • examples
    • context vectors
      • standard practice (e.g. LSA): make matrix of word counts, where each row is a word, and each column is a document
      • HD computing alternative: each row is a word, but each document is assigned a few ~10 columns at random
        • thus, the number of columns doesn’t scale with the number of documents
        • can also do this randomness for the rows (so the number of rows < the number of words)
        • can still get semantic vector for a row/column by adding together the rows/columns which are activated by that row/column
        • this examples still only uses bag-of-words (but can be extended to more)
    • learning rules by example
      • particular instance of a rule is a rule (e.g mother-son-baby $\to$ grandmother)
        • as we get more examples and average them, the rule gets better
        • doesn’t always work (especially when things collapse to identity rule)
    • analogies from pairs
      • ex. what is the dollar of mexico?

ex. identify the language

  • paper: LANGUAGE RECOGNITION USING RANDOM INDEXING (joshi et al. 2015)
  • benefits - very simple and scalable - only go through data once
    • equally easy to use 4-grams vs. 5-grams
  • data
    • train: given million bytes of text per language (in the same alphabet)
    • test: new sentences for each language
  • training: compute a 10k profile vector for each language and for each test sentence
    • could encode each letter wih a seed vector which is 10k
    • instead encode trigrams with rotate and multiply
      • 1st letter vec rotated by 2 * 2nd letter vec rotated by 1 * 3rd letter vec
      • ex. THE = r(r(T)) * r(H) * r(E)
      • approximately orthogonal to all the letter vectors and all the other possible trigram vectors…
    • profile = sum of all trigram vectors (taken sliding)
      • ex. banana = ban + ana + nan + ana
      • profile is like a histogram of trigrams
  • testing
    • compare each test sentence to profiles via dot product
    • clusters similar languages - cool!
    • gets 97% test acc
    • can query the letter most likely to follor “TH”
      • form query vector $Q = r(r(T)) * r(H)$
      • query by using multiply X + Q * english-profile-vec
      • find closest letter vecs to X - yields “e”

details

  • mathematical background
    • randomly chosen vecs are dissimilar
    • sum vector is similar to its argument vectors
    • product vector and permuted vector are dissimilar to their argument vectors
    • multiplication distibutes over addition
    • permutation distributes over both additions and multiplication
    • multiplication and permutations are invertible
    • addition is approximately invertible
  • comparison to DNNs
    • both do statistical learning from data
    • data can be noisy
    • both use high-dim vecs although DNNs get bad with him dims (e.g. 100k)
    • HD is founded on rich mathematical theory
    • new codewords are made from existing ones
    • HD memory is a separate func
    • HD algos are transparent, incremental (on-line), scalable
    • somewhat closer to the brain…cerebellum anatomy seems to be match HD
    • HD: holistic (distributed repr.) is robust
  • different names
    • Tony plate: holographic reduced representation
    • ross gayler: multiply-add-permute arch
    • gayler & levi: vector-symbolic arch
    • gallant & okaywe: matrix binding with additive termps
    • fourier holographic reduced reprsentations (FHRR; Plate)
    • …many more names
  • theory of sequence indexing and working memory in RNNs
    • trying to make key-value pairs
    • VSA as a structured approach for understanding neural networks
    • reservoir computing = state-dependent network = echos-state network = liquid state machine - try to represen sequential temporal data - builds representations on the fly

papers

dnns with memory

  • Neural Statistician (Edwards & Storkey, 2016) summarises a dataset by averaging over their embeddings
  • kanerva machine
    • like a VAE where the prior is derived from an adaptive memory store

visual sampling

dynamic routing between capsules

  • hinton 1981 - reference frames require structured representations
    • mapping units vote for different orientations, sizes, positions based on basic units
    • mapping units gate the activity from other types of units - weight is dependent on if mapping is activated
    • top-down activations give info back to mapping units
    • this is a hopfield net with three-way connections (between input units, output units, mapping units)
    • reference frame is a key part of how we see - need to vote for transformations
  • olshausen, anderson, & van essen 1993 - dynamic routing circuits
    • ran simulations of such things (hinton said it was hard to get simulations to work)
    • learn things in object-based reference frames
    • inputs -> outputs has weight matrix gated by control
  • zeiler & fergus 2013 - visualizing things at intermediate layers - deconv (by dynamic routing)
    • save indexes of max pooling (these would be the control neurons)
    • when you do deconv, assign max value to these indexes
  • arathom 02 - map-seeking circuits
  • tenenbaum & freeman 2000 - bilinear models
    • trying to separate content + style
  • hinton et al 2011 - transforming autoencoders - trained neural net to learn to shift imge
  • sabour et al 2017 - dynamic routing between capsules
    • units output a vector (represents info about reference frame)
    • matrix transforms reference frames between units
    • recurrent control units settle on some transformation to identify reference frame
  • notes from this blog post
    • problems with cnns
      • pooling loses info
      • don’t account for spatial relations between image parts
      • can’t transfer info to new viewpoints
    • capsule - vector specifying the features of an object (e.g. position, size, orientation, hue texture) and its likelihood
      • ex. an “eye” capsule could specify the probability it exists, its position, and its size
      • magnitude (i.e. length) of vector represents probability it exists (e.g. there is an eye)
      • direction of vector represents the instantiation parameters (e.g. position, size)
    • hierarchy
      • capsules in later layers are functions of the capsules in lower layers, and since capsule has extra properties can ask questions like “are both eyes similarly sized?”
        • equivariance = we can ensure our net is invariant to viewpoints by checking for all similar rotations/transformations in the same amount/direction
      • active capsules at one level make predictions for the instantiation parameters of higher-level capsules
        • when multiple predictions agree, a higher-level capsule is activated
    • steps in a capsule (e.g. one that recognizes faces)
      • receives an input vector (e.g. representing eye)
      • apply affine transformation - encodes spatial relationships (e.g. between eye and where the face should be)
      • applying weighted sum by the C weights, learned by the routing algorithm
        • these weights are learned to group similar outputs to make higher-level capsules
      • vectors are squashed so their magnitudes are between 0 and 1
      • outputs a vector

hierarchical temporal memory (htm)

  • binary synapses and learns by modeling the growth of new synapses and the decay of unused synapses
  • separate aspects of brains and neurons that are essential for intelligence from those that depend on brain implementation

necortical structure

  • evolution leads to physical/logical hierarchy of brain regions
  • neocortex is like a flat sheet
  • neocortex regions are similar and do similar computation
    • Mountcastle 1978: vision regions are vision becase they receive visual input
    • number of regions / connectivity seems to be genetic
  • before necortex, brain regions were homogenous: spinal cord, brain stem, basal ganglia, …
  • cortical_columns

principles

  • common algorithims accross neocortex
  • hierarchy
  • sparse distributed representations (SDR) - vectors with thousands of bits, mostly 0s
    • bits of representation encode semantic properties
  • inputs
    • data from the sense
    • copy of the motor commands
      • “sensory-motor” integration - perception is stable while the eyes move
  • patterns are constantly changing
  • necortex tries to control old brain regions which control muscles
  • learning: region accepts stream of sensory data + motor commands
    • learns of changes in inputs
    • ouputs motor commands
    • only knows how its output changes its input
    • must learn how to control behavior via associative linking
  • sensory encoders - takes input and turnes it into an SDR
    • engineered systems can use non-human senses
  • behavior needs to be incorporated fully
  • temporal memory - is a memory of sequences
    • everything the neocortex does is based on memory and recall of sequences of patterns
  • on-line learning
    • prediction is compared to what actually happens and forms the basis of learning
    • minimize the error of predictions

papers

  • “A Theory of How Columns in the Neocortex Enable Learning the Structure of the World”
    • network model that learns the structure of objects through movement
    • object recognition
      • over time individual columns integrate changing inputs to recognize complete objects
      • through existing lateral connections
    • within each column, neocortex is calculating a location representation
      • locations relative to each other = allocentric
    • much more motion involved
    • multiple columns - integrate spatial inputs - make things fast
    • single column - integrate touches over time - represent objects properly
  • “Why Neurons Have Thousands of Synapses, A Theory of Sequence Memory in Neocortex”
    • learning and recalling sequences of patterns
    • neuron with lots of synapses can learn transitions of patterns
    • network of these can form robust memory

forgetting

  • Continual Lifelong Learning with Neural Networks: A Review
    • main issues is catastrophic forgetting / stability-plasticity dilemma
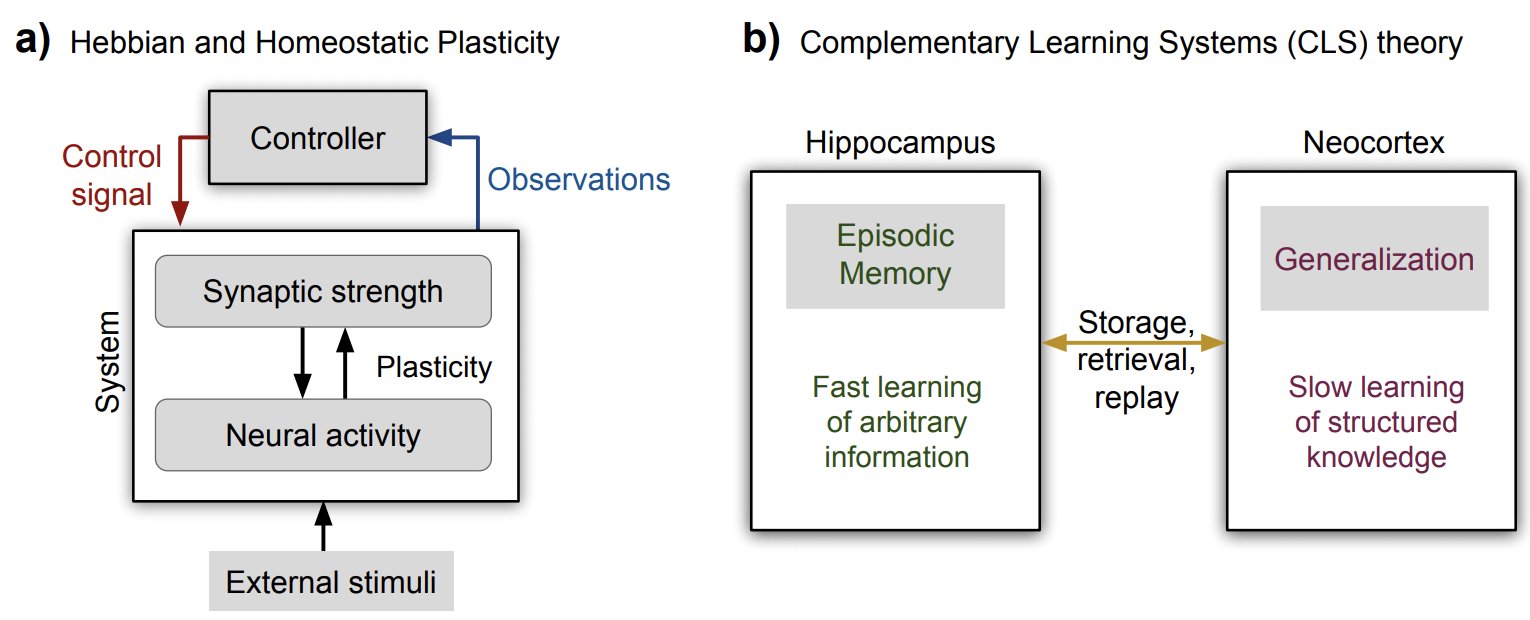
    • Screen Shot 2020-01-01 at 11.49.32 AM
    • 2 types of plasticity
      • Hebbian plasticity (Hebb 1949) for positive feedback instability
      • compensatory homeostatic plasticity which stabilizes neural activity
    • approaches: regularization, dynamic architectures (e.g. add more nodes after each task), memory replay

deeptune-style

  • ponce_19_evolving_stimuli: https://www.cell.com/action/showPdf?pii=S0092-8674%2819%2930391-5
  • bashivan_18_ann_synthesis
  • adept paper
    • use kernel regression from CNN embedding to calculate distances between preset images
    • select preset images
    • verified with macaque v4 recording
    • currently only study that optimizes firing rates of multiple neurons
      • pick next stimulus in closed-loop (“adaptive sampling” = “optimal experimental design”)
  • J. Benda, T. Gollisch, C. K. Machens, and A. V. Herz, “From response to stimulus: adaptive sampling in sensory physiology”

    • find the smallest number of stimuli needed to fit parameters of a model that predicts the recorded neuron’s activity from the stimulus

    • maximizing firing rates via genetic algorithms

    • maximizing firing rate via gradient ascent

  • C. DiMattina and K. Zhang,“Adaptive stimulus optimization for sensory systems neuroscience”](https://www.frontiersin.org/articles/10.3389/fncir.2013.00101/full)

    • 2 general approaches: gradient-based approaches + genetic algorithms
    • can put constraints on stimulus space
    • stimulus adaptation
    • might want iso-response surfaces
    • maximally informative stimulus ensembles (Machens, 2002)
    • model-fitting: pick to maximize info-gain w/ model params
    • using fixed stimulus sets like white noise may be deeply problematic for efforts to identify non-linear hierarchical network models due to continuous parameter confounding (DiMattina and Zhang, 2010)
    • use for model selection

population coding

  • saxena_19_pop_cunningham: “Towards the neural population doctrine”
    • correlated trial-to-trial variability
      • Ni et al. showed that the correlated variability in V4 neurons during attention and learning — processes that have inherently different timescales — robustly decreases
      • ‘choice’ decoder built on neural activity in the first PC performs as well as one built on the full dataset, suggesting that the relationship of neural variability to behavior lies in a relatively small subspace of the state space.
    • decoding
      • more neurons only helps if neuron doesn’t lie in span of previous neurons
    • encoding
      • can train dnn goal-driven or train dnn on the neural responses directly
    • testing
      • important to be able to test population structure directly
  • population vector coding - ex. neurons coded for direction sum to get final direction
  • reduces uncertainty
  • correlation coding - correlations betweeen spikes carries extra info
  • independent-spike coding - each spike is independent of other spikes within the spike train
  • position coding - want to represent a position
    • for grid cells, very efficient
  • sparse coding
  • hard when noise between neurons is correlated
  • measures of information
  • eda
    • plot neuron responses
    • calc neuron covariances

interesting misc papers

  • berardino 17 eigendistortions
    • Fisher info matrix under certain assumptions = $Jacob^TJacob$ (pixels x pixels) where Jacob is the Jacobian matrix for the function f action on the pixels x
    • most and least noticeable distortion directions corresponding to the eigenvectors of the Fisher info matrix
  • gao_19_v1_repr
    • don’t learn from images - v1 repr should come from motion like it does in the real world
    • repr
      • vector of local content
      • matrix of local displacement
    • why is this repr nice?
      • separate reps of static image content and change due to motion
      • disentangled rotations
    • learning
      • predict next image given current image + displacement field
      • predict next image vector given current frame vectors + displacement
  • kietzmann_18_dnn_in_neuro_rvw
  • friston_10_free_energy
    • friston_free_energy